
circleToy
The best cure for a flat map is a toy, one that undoes the flatness,
and grants us liberty to explore the many relations and scales of
organizational structure, connectivity, and unity. Such a toy, properly
crafted and generously employed, allows us to more accurately understand
our own potentials and position in the incredible diversity of biocognitive
organization that is our living world. These birthrights don’t
belong to the few, or the privileged. They are instead the birthrights
of children. They comprise the bioevolutionary inheritance of every
living organism, and when they are occluded or denied, whole encyclopedias
of confusion, cataclysm and atrocity ensue, echoing aperiodically
over time. This is not ‘the way Life is’ — but
it can be the way Life is when we allow our animalian and cognitive
features of origin and connectivity to be lost in maps and metaphors
of relation that are by their natures cognitively or biologically
predatory. That a map or metaphor may be predatory isn’t a
common concept, but as we proceed — in turns and cones —
we will come to see that most of the dominant metaphors in society
actually act like organisms. They vie constantly for ownership,
control and dominion in the oceans and terrains of human sentience.
The right toys will generally aid us in discovering, understanding
and expressing our potentials. The wrong toys will consistently
steal our potential energy for their own elaboration, fortification,
and distribution to others. This is a rule that applies to nearly
any form of toy we might name, but perhaps especially to language,
metaphors, and logics. Toys with which we can organize our understandings
of the features of living systems, and their abilities to generate
new ways of knowing, provide what I believe in my heart and mind
to be the finest of possible riches. All of our hopes and dreams
as a species, depend entirely upon a real experiential access to
our natures and origins as lifeForms. These abilities are thousands
of scales beyond the wildest of our fictions, or religions. They
are dormant, and uniquely embodied in every form of life, but in
humans, in particular, they achieve a rare complexity, and an even
more valuable terrain of connectivities.
The first one I will explore is related to an important root-feature
of the modes of organization not only of Nature, but of cognition
as well. It is a context of biology, science, magic, physics, and
language alike, and is reflected uniquely in each of them. This
feature, which is something like a transport of structurally emergent
relation, is reminiscent of the way in which the potential energy
of vacuum has implications for the organization of matter that will
arise and exist in specialized congruence with its contexts and
relations. I call this feature scalarity, which means, in essence,
the contextually sensitive connectivity between scales of organization
— related to structural establishment, modulation, elaboration
or emergence.
In a sense, Life, and cognition, are games of scalarity —
they exit as momentary structures of the relation of many scales
of organization and interscalar relational activity at any given
scale or apparent unity — such as a human being, or an ecosystem.
And it isn’t exactly missing — we’re aware of
this metaphor, but the importance we ascribe to it fails to grant
us experiential access to its real treasures.
The idea of scalarity has been around almost forever, so to speak.
At least as long as the shell of the chambered nautilus. We keep
dressing it up differently, however. When we dress it up wrong,
we end up looking at a very complex token, instead of experiencing
a relationShip. Toys can help us reMember these relationships, and
grant us some interesting spontaneous modeling tools, as well.
trees
The metaphor we most commonly employ for the general shape of the
expressive epic of creatureForm evolution is the Tree. We’ve
got basically three possible ideas about Life’s arisal on
Earth: Seed (intrusive fertilization), Emergence (self-organizing
chemistries in context), and Decree (creation). Given the current
status of our understandings of biological scale and reality, specifically
including a noticing of character and emotion in Nature, we find
none of them improbable, and an integration of all three the more
likely model. Regardless of this, we can make a toy where either
a single form of cellular or proto-cellular life or a set of different
events resulted in the arisal of diverse cellular cultures, over
time.
Judging from what we can observe and infer, it seems likely that
complex forms were assembled from highly specialized sub-forms,
in nearly all instances, with the general goal being the localized
availability of many diversely connective transports and libraries
of evolutionarily conserved complexity. Eventually, more complex
associations became first possible, then probable, and then reality.
We metaphy this process with a kind of flat tree showing speciation.
From an as yet unknown seed, a root appears, a stalk, and then branches.
We end up, for the moment, with something like the tree-pattern
in the example below, taken from here
— where there’s an interesting discussion of evolutionary
generalists vs specialists and their effects on novel mutations,
or species.
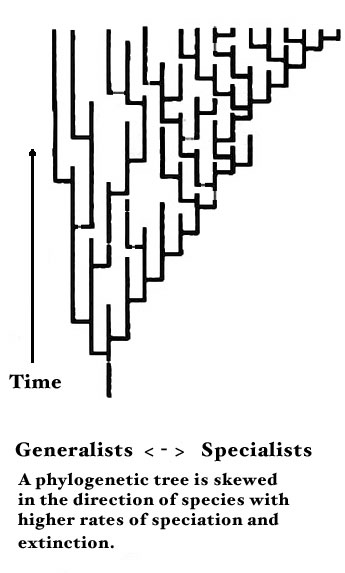
The metaphor is one of a flat tree, and this is the mode of mapping
we commonly utilize in describing it.More specifically, thanks to
the work of Carl Woese and many other genetic biologists, we have
a tree showing our classifications and theoretical anscestry. Here’s
a simplified version for reference:
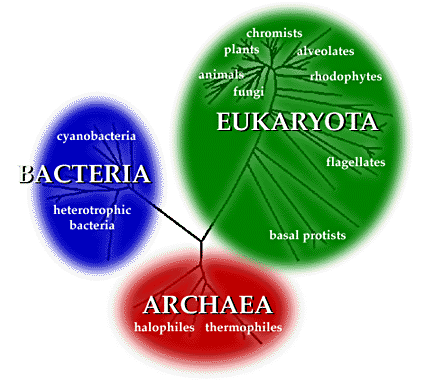
Even as a flat map of a tree-like arrangement of classes, we can
see that this model has an interesting quality: it gains branches
and detail if we ‘zoom in‘ with our perspective, revealing
greater diversity, and it simplifies itself again as we zoom out.
If we considered every unique phylogenetic or phyiscal trait as
an individual, the tree of life would be almost nothing but branches
— there would be related groups, but there would always be
some uniquely local diversity ‘left over’ no matter
how rigorous our classifications. Yet, the Tree model is essentially
a decent metaphor, even though it lacks overt scalarity. For example,
we can zoom in to see detail with our imagination, but this feature
is in no way implied by the map above — we have to discuss
it to notice it, which, in essence, means we have to have a specific
domain of additional knowledge to recognize this feature clearly.
It isn’t really part of the metaphor. Also, time is missing
— all organisms are included or includible in such a tree,
and there’s no obvious termporal feature of the map.
Lately, we’ve begun to modulate our ways of making trees,
which is a positive step. Here’s an example of a similar but
perhaps more useful species of tree-map:
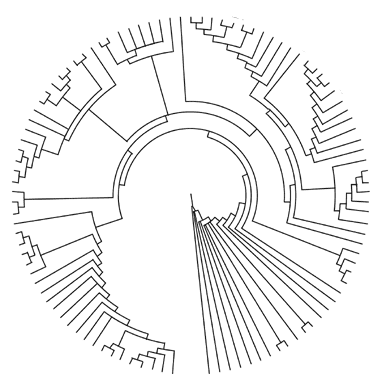
A circular map (or metpahor) is essentially more useful for a variety
of reasons, but chief amongst them is that it can more accurately
imply temporal relation (at least in concert with a linear temporal
metaphor). As part of an exploration-toy, we could place the progenitor-organism
at the core, adjust the map as we learn, and arrive with a useful
(but still flat) model of evolution’s relation with organismal
diversification. This tree-map also elaborates into many branchlets
if we zoom in, and simplifies (as well as unifies) when we zoom
out with our perspective on classes,members — and size. I’m
not recommending we toss our linear tree-maps, only that we explore
and integrate the alternatives in an effort to free us from flatness.
The best thing about the map above, is that if we merely pull the
core away from the plane — we get a cone. This is a majestic
improvement.
slideRule, v 2: the rabbitHole
By way of beginnings, we will create an imaginary and general ‘measuring
toy’. In a sense, we are going to re-invent the ruler. Ours
will be conical, and represent something of a slide-rule, as well.
It can also act like a strange clock. A clock of scales.
Let’s take a large clock-face, say 2 feet in diameter, and
paint 12 lines emanating from a blue
dot at the center to a red
ring at the face’s edge. We’ll arrange rays at
30-degree angles starting at 0 (12-o’clock). This is essentially
what we have in a clock, except the rays are numbered —ours
are just lines from the point to the ring. We end up with a flat
pie, with a dot in the middle, divided into 12 slices.
If we lay the clock flat on the floor and pull the point upward,
we can stretch our imaginary clockface into a cone. The outer edge
of the clock becomes the base (or lip), and the dot in the center
as the point (or tip). The rays now run along the cone from the
ring to point. Left as is, we have a common, straight cone, if we
vacuum a little of the cone’s volume away, we can have a fluted
cone. For ease of reference, we’ll posit our cone as standing
on the floor next to us, and being about half our body-size —
so that we may look at it easily from any side. Or we can look straight
down onto the cone from directly above the point.
Our first addition to our toy will be a spiral line, which, from
0/12-o’clock upon the base will circle the cone a given number
of times (in any real application) before reaching the point at
(x/12-o’clock). To this imaginary assemblage, we will add
a given number of rings, which we can slide to any position on the
cone, to indicate a ‘scale’ of some sort. The base ring
(red) will always function as the the
largest and most inclusive ring in any model we build.
When we slide one of our rings along the cone, it will shrink if
moved upward (as the volume of the cone shrinks), and expand appropriately
if moved down toward the ring. In our imaginary model, we can shift
the relations of the spiral and/or the rings at will, adjusting
them as we desire to generally indicate relations of scale. In a
linear expression of relation amongst the rings, they would be arranged
equidistantly along the cone. In a non-linear map, their spacing
would be asymmetric, but perhaps in algorithmic relation to each
other along the cone’s length. We can now begin to paint our
model with information, and thus create a instance of an actual
map of scalar relation
We have now crafted a very general template of a mapping-toy. Any
actual instance of a real (though imaginary) map will involve adding
rings of scale, saying what they denote, and moving the rings and
adjusting our spiral to match our desires on the cone. We can create
a real map as an example of how our toy relates to what I am referring
to as a linked set of scales. For the moment, we’ll imagine
that our cone is transparent, and has at its base a flat plate which
can move up and down inside the cone, shrinking or expanding in
diameter as it does so. On this plate is a clock-arm, anchored to
the plate’s center, and this arm revolves around this point.
We will divide our cone into three scales, by placing two rings
equidistantly along its length. We have twelve rays around the cone,
like the hour positions on our common round clocks.We then add our
spiral, whose first circuit (leaving the base at 12 o’clock)
repeats at the first ring at 12, (1/3rd of the way up the cone)
again at the second ring at 12 (2/3rds up), and its third circuit
is completed at 12 where it joins the cone’s point.
Now we can set our strange clock in motion. The hand starts at
scale (0), 12-o’clock on the base ring. As it moves toward
(0) 1 o’clock (following the rise of the spiral), the plate
upon which the hand is fixed rises, shrinking inside the cone as
it does so. When the hand reaches the (0)1-o’clock position,
it has risen 1/12th of the way to the next scale, and the length
of the hand (which is equivalent to the radius of the cone at this
scale) has decreased. As conical time progresses, eventually the
hand and its shrinking plate will disappear into the point, at the
moment it attempts to move forward from the (3)12-o’clock
position. One pass up or down the cone results in 3 scales of the
repetition of a 12-part cycle.
paint
the ruler Green
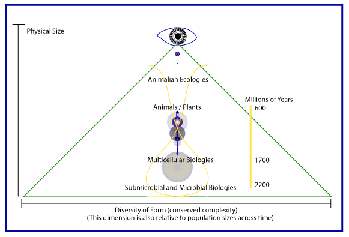
[click
to enlarge]
Let us explore our toy by mapping some features of Life’s
organization on its scalarly divisible surface. If we were to divide
the scales of Life on Earth into an order based upon the physical
size of participants on a scale of size or mass, we might end up
with a list something like this:
1. proto-life/virii
2. cells
3. multicellular animal
4. tinyAnimal
5. insect
6. reptile/fish/bird
7. mammals/animals
In arranging these on our map, we don’t have to be mathematically
precise — we’re just learning how to play with our toy.
We must first decide where to place the index — at the
base or tip. In this case, the tip is smaller, and we will place
scale 1 near the point to indicate a smaller size (the reverse of
this option is also interesting).
The first four rings would be very near the tip, and the next three
would be closely spaced together near the bottom ring, which represents
scale 7. Our spiral would form a 4-scale spring, a long winding
line, and the a 3-scale spring near the base. Not terribly interesting
by itself, but let’s examine some of the features of our first
map. Firstly we can speculate that the next ‘size’ of
Life might be an ecosystem — but this is never specifically
embodied — it is a connectivity-organism, making it hard to
place at a specific size-scale. There is another reason we would
have difficulty placing en ecosystem upon our cone at a specific
location, which is that it isn’t really a scale at all —
it’s a principle of organization. As such, it exists above
and at each of the scales as an embodied potential. It is also represented
within almost all of the scales (inside a participant). We could
say it is the metascale of our first cone. Here we see what the
‘meta’ means — to be embodied in scales, within
oneself.
Where the ecosystem is a general metascale, the biosphere is a specific
one. From a semantic basis of separate identity, we see a specific
biosphere — Earth. Switching to one of general connectivity,
we see an ecosystem — Life. These then are two of the primary
principles of organization which our strange map integrates.
Let’s preserve this cone of sizes, and create a second version.
In this version, we’ll arrange each scale according to evolutionary
age. We’ll use data from the book What is Life, by Lynn Margulis
and Dorian Sagan to find general locations on our cone representing
the phases of arisal in linear time. We will thus presume that the
physical Earth is some 4600 million years old and that biological
precursors likely appeared around 3900 million years ago. For this
model, we’ll re-arrange our list a bit as shown below. The
7th scale is at the base of our cone at the bottom ring. The percentage
above each scale indicates how far up the cone we place the rings,
and where the circuits of our spiral lie upon their scales. For
reference, the estimated emergence of our most ancient human ancestors
is indicated at the top of the list.
(humans: 99.999 ~4 mY ago)
99.8%: 290 mY ago
1. mammals/animals
92.6%: 300 mY ago
2. reptile/fish
85.6%: ~570 mY ago
3. insect
85.5%: ~580 mY ago
4. tinyAnimal
85%: ~600 mY ago
5. multicellular animal
2.6%: ~3800 mY ago
6 cell
0%:Base: ~4000 mY ago
7. proto-life/virii
With scale 7 as the base-ring, scale 6 would be very close, but
perceptibly distinct. Additionally, these two scales have been evolving
in concert with the local biosphere for the entirety of the
cone, and nothing else even shows up until 82% up the cone
toward the tip.
So our seven scales would be arranged with two near the ring, and
the rest very close to the tip. The emergence of our species would
not be visible, it would be too close to the modern moment at the
top of the cone. In terms of time as a process of terrestrial evolution,
we don’t even qualify as infants. Parenthetically, our relationship
with a living world as enlanguaged humans has barely begun in this
context.
The human position is unique, we are a kind of metacreature,
in the way that an ecosystem is a metascale. We contain and emerge
from myriads of scalar conservations and activities in all the domains
beneath and around us in the cone. I believe that we represent them,
as well, for we are their most precious organizational success,
and every sacrifice possible has and is being made to sustain us.
Our species is then favored — by the lineages of
biocognitive relation and conservation which our existence and activity
represent. To us, it is given to elaborate the essential contexts
and subjects of biocognition, and understanding. Our place at the
top of the cone is essentially sacred, and we are probably the first
separate animal to embody such potentials in the Earth’s herstory.
Let’s craft a final map, this one of populations on Earth
at sizes. Interestingly, although sizes and ages are, at the scale
of our map, relatively constant — populations are not. If
we could zoom in close enough, we’d see waves of populations
and interactive dynamics consistently communicated up and down the
spiral, and the rings at each scale would move while we observed,
however the rings of the small would move more wildly, and probably
in cycles related to terrestrial and solar-terrestrial relationships
In our final map, which is a highly speculative one
in terms of actual sizes, we could presume that the base is again
7. From there all of the scales other than 7 would be wound into
an invisible spring near the tip, like eyes atop myriads of blind
living pyramids. From one perspective, our own species is the eye
atop the pyramid of eyes — Earth’s first metacreature.
Possibly her last. But if we were assembled by something, it appears
that this something drove cellular biologies to assemble it. If
not, they assembled it at random, which seems incongruent with our
experience, and my own essential sense of what is reasonable. I
like to believe there is something I would call cellular intention,
from which the general and specific adaptations of evolution accrue
their spectacular character. At the root of this are elemental imperatives,
and in examining some of these as we proceed, we we will cause for
wonder, and celebration. I hope we shall also find cause for a unity
of action and understanding as well.
There are many important symmetries we may notice
when playing liberally with such a toy. We do not suddenly become
immune to the experience of a flat map, but we begin to realize
the power of connecting maps of different scales of perspective
or frequency into a spiral of unity. Each position above the smallest
contains most of what is beneath or below it in all of our models.
Each ring of scale leads to a cone at its own scale, and thus our
map is actually ‘filled with maps like itself’. Each
participant, at any scale, is also organized thus, as a local cone
of scalar symmetries. We will explore this relation between our
maps and of living systems — and later cognitive systems —
as we proceed. The relation between the scales is not one-way or
linear, neither in organization, nor influence. The connectivities
across scales are, themselves, multi-scalar.
We, as biocognitive Life, are something we have not
yet imagined as adults. We have glanced in the direction of our
terrestrial heritage, but have never understood what we see there.
The truth is hard to swallow, for what we actually are is more than
all our stories combined. We would probably not believe in it, unless
we experience it directly. It is my hope that by looking at some
relations and questions, we can have a lot more of that experience,
and a lot less of its opposite, and the outcomes which thereby emerge.
o:O:o
|